(Fast) alles über Sudokus

Hier findet Ihr Tipps zum Lösen von Sudokus und ein paar Informationen mehr.



Vorwörtchen

Sudoku ist eigentlich ganz einfach, ....wenn man es oft genug gespielt hat.

• Die erste Maxime ist „Übung macht den Meister“.
• Zweitens: Jeder kann es lernen, vorausgesetzt man kann bis 9 zählen.
• Drittens: Lang genug geschwätzt, los geht’s:

Geschichte des Sudoku in Kurzform

Der Schweizer Mathematiker Leonhardt Euler erfand im 18. Jh. sogenannte Lateinische Quadrate. Ob sie die Grundlage für das Zahlenpuzzle „Number Place“ in den USA war, ist mir nicht bekannt. Die Japaner übernahmen das Rätsel, dieses wurden aufgepeppt, d.h. kniffliger gemacht. Seit den 90er Jahren gehört es in Japan zu den beliebtesten Spielen, hier bekam es auch seinen Namen. Seit 2004 wird es in Europa verbreitet gespielt und seit kurzem bin endlich auch ich ihm verfallen. ;-))

Werkzeuge

Überall finden sich heutzutage Sudokus. In diversen Zeitschriften, Tageszeitungen, als Rätselhefte in den entsprechenden Supermarktabteilungen oder ganze Bücher im Buchhandel. Neulich sogar als Sonderangebot beim Lidl. Wenn man die Wahl hat, sollte man nur die Rätsel aussuchen, die ausreichend große Kästchen haben. In die man auch mehrere Ziffern auf einmal eintragen kann. Auch auf das Papier sei zu achten. Es muß relativ radiergummiresistent sein, sonst sind Löcher vorprogrammiert. Das wichtigste Handwerkszeug: Bleistift und Radiergummi.



Ein Tipp für ganz Eifrige: das Sudoku mit entsprechend großen Kästchen auf einen Schreibblock übertragen, dann aber mit Kugelschreiber, damit man im Eifer des Gefechts nicht die Linien und vorgegebenen Zahlen weg radiert. Das macht mehr Arbeit und sollte nur bei schwierigen Rätseln gemacht werden.

Aufbau eines normalen (klassischen) Sudokus

Ein normales Sudoku hat 81 Kästchen: 9 waagerecht, 9 senkrecht. Diese 81 sind in 9 Karrees zu je 9 Kästchen (9er-Blöcke) unterteilt. In diesen befinden sich einige Zahlen (Minimum 17), die vorgegeben sind und die die Voraussetzung zum Lösen des Sudokus sind.

Varianten

Minisudokus mit kleineren Zahlenreihen, z.B. 4x4 Kästchen oder 6x6er. Diese sind besonders für absolute Anfänger oder Kinder geeignet. Ich habe auch mit diesen angefangen und mich dann hochgearbeitet.

Die Karrees sind nicht quadratisch sondern puzzleartig unregelmäßig (Freiform-Sudokus)

Diagonal-Sudoku sind klassische Sudokus, in denen in beiden Mitteldiagonalen die Zahlen auch nur je ein Mal vorkommen.

Die letzten beiden Varianten erleichtern das Lösen.

Buchstaben oder Symbole anstelle von Zahlen (Symbole trainieren das Gedächtnis und machen es somit schwieriger.)

Riesensudokus mit größeren Zahlenreihen

Abweichungen von der Grundregel

Grundregeln

Es gibt nur drei Grundregeln:

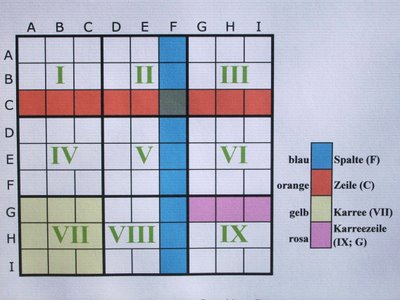
• In jeder Zeile (Waagerechte) darf jede Zahl nur einmal vorkommen.
• In jeder Spalte (Senkrechte) darf jede Zahl nur einmal vorkommen.
• In jedem Karree (9er-Block) darf jede Zahl nur einmal vorkommen.

Zeile, Spalte und Karree bilden je eine Reiheneinheit, die die Zahlen von 1 bis 9 in unterschiedlicher Folge enthalten.

Lösungswege
(davon gibt es unzählige. Hier der Weg, den ich verfolge:)

Los geht’s:

Beginnen Sie mit der 1 und überprüfen Sie alle Einsen daraufhin, ob sie zum Finden einer weiteren 1 geeignet sind. Dazu geht man die drei Karrees übereinander bzw. nebeneinander durch. In diesen Karrees müssen jeweils drei Einsen stehen. In der Zeile (oder Spalte), in der die 1 fehlt überprüft man nun, ob man die Position der 1 eindeutig bestimmen kann. Hierzu überprüft man die anderen beiden Karrees. Das heißt, hat man die Karrees in der Waagerechten angesehen, kann man nun die Senkrechten kontrollieren.

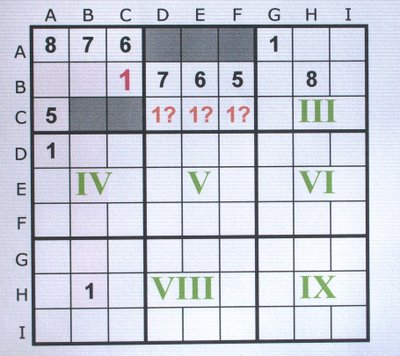
Benennen wir die Karrees mit römischen Ziffern I bis IX, und die Zeilen und Spalten eines Karrees als Karreezeile bzw. –spalte. Letztere bestehen aus jeweils drei Kästchen.

Siehe Abbildung oben.

Steht in II und III eine 1, aber in Karree I nicht, sieht man nach ob in IV und VII ebenfalls Einsen stehen. Wenn das der Fall ist kann man die Position für die fehlende 1 genau bestimmen. Die Zahl kann auch bestimmt werden, wenn z.B. nur in VII die Position deren 1 bekannt ist. Nämlich dann, wenn die in Frage kommenden Positionen durch andere vorgegebene Zahlen besetzt sind. Ist die Position nicht eindeutig feststellbar, stellt man diese erst einmal zurück, dann geht man die übrigen Karrees ohne 1 durch. Alle eindeutig bestimmbaren 1 werden an ihre Position eingetragen. Oft ergibt sich auch, nachdem man eine Zahl eindeutig bestimmt hat, die Position der betreffenden Ziffer im Nachbarkarree. Deshalb lohnt sich eine Nachkontrolle. Danach verfährt man mit den Zahlen 2 bis 9 genauso. Auf diese Art und Weise findet man mehr oder weniger Zahlen. Je weniger, desto kniffliger ist meistens das Sudoku.

Tipp: man geht jede Zahl nacheinander durch, so geht man sicher, daß man keine vergißt.

Danach überprüft man erneut jede einzelne Zahl, mit der 1 beginnend durch. Durch den Eintrag der beim ersten „Durchlauf“ gefundenen Zahlen ergeben sich möglicherweise nun eindeutige Positionen für einige weitere Zahlen, die man jetzt ausfüllen kann.

Tipp: Hat man eine Zahl für alle Karrees gefunden, kann man sie sich am Rande notieren, damit man diese beim nächsten Durchlauf nicht noch mal durchgeht.

Besser natürlich, man merkt sich’s. Sind nur ein oder zwei Exemplare einer Zahl vorgegeben oder fehlt sie völlig, dann deutet das auf einige Arbeit hin.

Irgendwann, spätestens nach dem dritten Durchlauf, kommt man an einen Punkt, wo man keine offensichtlich eindeutige Position für seine Zahlen findet. Jetzt ist Logik gefragt.

Tipp: Kontrollieren sie ab und zu ihre Karrees, Zeilen oder Spalten, ob sie nicht versehentlich Zahlen doppelt enthalten. Das kann durchaus mal im Eifer des Gefechts passieren. Dann wird das Sudoku falsch. Man muß alle Zahlen bis zu dem gemachten Fehler zurückverfolgen und ausradieren, wenn man das nicht mehr weiß, kann man noch mal von vorn anfangen. Pech gehabt!

Für EIN Sudoku gibt es immer nur EINE Lösung.

Als nächstes suchen Sie sich die Zeilen oder Spalten oder Karrees, die die meisten Zahlen enthalten. Die Leerkästchen überprüft man auf mögliche Zahlenkandidaten. Bei nur einem Leerkästchen ist die Zahl von vornherein deutig. Bei zwei Leerkästchen ist die Chance ebenfalls groß, die gesuchten Zahlen zuzuordnen. Wenn nicht, dann trägt man die beiden Kandidaten klein mit Bleistift in beide Kästchen ein. So geht man Spalte für Spalte, Zeile für Zeile und Karree für Karree durch. Trägt die jeweils fehlenden, in Frage kommenden Ziffern klein ein. (über diese Notizen mehr weiter unten).

Tipp: Man sollte so lange wie möglich ohne diese Hilfszahlen auskommen und versuchen mit Logik vorwärts zu kommen.

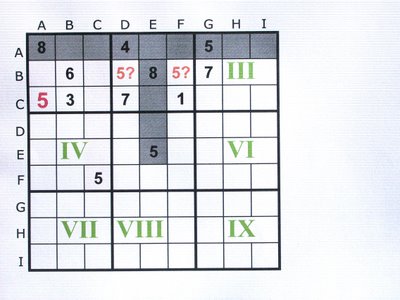
In drei neben- (oder über-)einander liegenden Karrees gibt es von einer Zahl nur einen Vertreter, z.B. Karree III enthält eine 1 in Zeile A. In den beiden waagerecht benachbarten Karrees ist die Position der Einsen nicht bekannt. Aber in Karree II ist eine waagerechte Karreezeile komplett mit Zahlen belegt, im Beispiel die Zeile B, folglich muß diesem Karree II eine 1 irgendwo in Zeile C stehen, weil ja Zeile B belegt ist und Karreezeile A von keiner 1 mehr belegt werden darf. Für Karree I bleibt nur noch die Zeile B übrig, in der eine 1 hineinpaßt. Jetzt überprüft man die Spalten der dazugehörigen senkrechten Karrees auf eine Möglichkeit, diese 1en eindeutig zuordnen zu können. Hierzu überprüft man die darunter liegenden Karrees IV und VII.

Fehlen in einer Spalte (oder Zeile) nur noch 2 Zahlen und befinden sich diese zwei fehlenden Zahlen in einem Karree, so sind diese beiden Zahlen auf diese beiden Kästchen beschränkt. Demzufolge lassen sich die übrigen Leerkästchen dieses Karrees etwas leichter bestimmen.
Ist außer den beiden Kästchen nur noch eines leer, dann ist die gesuchte Zahl eindeutig.
In Karree II sind zwei Zahlen der Reihe C bekannt (7 und 1). Man sucht in den darunter liegenden Karrees (V und VIII) eine Zahl, die die oben fehlende ausschließt, hier eine 5 in Karree V. Somit kann man diese Karreezeile vorläufig als voll betrachten. In Karree III ist die Zahl 5 in Zeile A vorgegeben. Also muß in Karreezeile (II;B) in einer der beiden leeren Kästchen auf alle Fälle eine 5 stehen. Karreezeile (I;B) ist damit ausgeschlossen, also muß in Karree I die gesuchte 5 in Zeile C stehen. Die 5 kann durch eine weitere 5 in Spalte C (senkrecht) in Karree IV für Spalte A in Zeile C festgelegt werden.

Man sucht sich ein leeres Kästchen, bei dem sich eine Zeile und Spalte kreuzen, die besonders viele Zahlen schon enthalten. Man überprüft diese und findet so vielleicht die gesuchte Zahl, weil es die einzige ist, die in beiden Reiheneinheiten nicht vorkommt.
Nach der indirekten Bestimmung sind wieder neue Zahlen eingetragen. Jetzt könnte man einen neuen Durchlauf starten. Mit Sicherheit (hoffentlich) findet man noch mal ein oder zwei neue Ziffern.
Hat man vermeintlich alle Möglichkeiten zur Bestimmung der leeren Kästchen ausprobiert, bleibt einem dann nur noch das Eintragen der möglichen Zahlen in das leere Kästchen.

Notizzahlen:
Ich nenne diese Hilfszahlen hier mal Notizzahlen. Es könnte theoretisch sein, daß man dann 5 und mehr Zahlen eintragen muß, das passiert bei besonders kniffligen Rätseln oder wenn man bei der direkten Zahlenbestimmung nicht gründlich genug gearbeitet hat.
Mein eingangs gegebener Hinweis, Sudokus mit schön großen Feldern zu wählen, damit alle Notizzahlen Platz haben, erweist sich hier als Vorteil. Stehen die Notizzahlen nämlich zu eng, radiert man leicht versehentlich mehr Zahlen als geplant weg.
Dann vergleicht man jede Zeile, Spalte und jedes Karree auf Zahlen, die nur einmal in der jeweiligen Reiheneinheit vorkommen.
Hat man so eine Zahl gefunden, radiert man die übrigen Zahlen aus diesem Kästchen oder streicht sie aus.
Das kommt nicht allzu häufig vor, weil man ja eigentlich schon mit der direkter Zahlenbestimmung vorgearbeitet hat.
Des weiteren sucht man Zahlenpärchen, die in einer Reiheneinheit nur 2x auftreten.

Beispiel:
In fünf leeren Kästchen einer Einheit stehen die Notizzahlen: 1234; 134; 12; 12; 25
Die 5 kommt nur einmal vor, demnach kommt in dieses Kästchen mit Sicherheit die 5. Man kann die Zwei aus diesem Kästchen entfernen.
Die Ziffern 3 und 4 kommen nur zweimal und jeweils gemeinsam vor, also bilden diese beiden Ziffern ein Paar. Man weiß nun: diese beiden Kästchen sind durch die Zahlen 3 und 4 belegt, auch wenn nicht genau, welche von beiden in welches Kästchen gehört. Die 1 und 2 in den ersten beiden Kästchen können ausradiert werden.
Es bleiben die 1 und 2 in zwei Kästchen übrig.

Nun kann man die betroffenen beiden anderen Reiheneinheiten auf die geänderten Notizzahlenverhältnisse kontrollieren, in der Hoffnung, daß nun weitere Zahlen eindeutig bestimmt werden können.

Es ist notwendig, Zeile für Zeile, Spalte für Spalte und Karree für Karree zu kontrollieren. Man kommt nicht drum herum, das mehrmals zu tun, denn jede Änderung bei den Zahlen ergibt neue Konstellationen, die überprüft werden muß.

Auch kommt es durchaus vor, daß man vergessen hat, eine Notizzahl auszuradieren. Dann kommt man nicht weiter. Daher ist viel Geduld bei den erneuten Kontrollen erforderlich.

Tipp: Hilfreich ist es auch, wenn man mal nicht weiter kommt, das Sudoku für eine Weile wegzulegen. Ich nehme das Sudoku erst dann wieder zur Hand, wenn ich inzwischen andere gelöst habe.

Ein gutes Sudoku ist normalerweise immer durch Logik eindeutig lösbar.

Es kann aber durchaus auch vorkommen, daß man an einen Punkt kommt, wo man überhaupt nicht mehr weiterkommt.
Dann bleibt einem nur noch das Ausprobieren.
Ich habe bei ca. 100 gelösten Sudokus diese Methode bisher nur einmal anwenden müssen.
Man geht die Varianten durch, eine wird dann passen. Pech, wenn es ausgerechnet die letzte ist.
Macht man es im Kopf, trainiert es das Gedächtnis.
Ich gebe zu, ich habe mir Notizen gemacht, aber das brauche ich ja niemandem zu erzählen.


So, jetzt wünsche ich viel Spaß beim Lösen Eurer Sudokus.
Sollte ich noch weitere Tricks herausfinden, werde ich sie Euch wissen lassen.